Uno de los videojuegos más populares en los últimos tiempos es Minecraft, creado en 2009 por el sueco Notch (seudónimo de Markus Alexej Persson).
Desde entonces, se ha convertido en un auténtico fenómeno social. Una de las características que diferencian este juego de los tradicionales es que no es competitivo, sino colaborativo. Y es de los llamados de «mundo abierto»: los jugadores pueden moverse como deseen en un mundo virtual y compartir objetivos.
El jugador puede ir colocando o destruyendo bloques tridimensionales cúbicos que tienen unas dimensiones fijas, pero pueden representar diferentes elementos como piedras, minerales o troncos.
Algunas de estas características han sido percibidas por muchos profesores como un potencial recurso educativo. Por ello, han fundado una plataforma gratuita en la que comparten las actividades que han diseñado en los más diversos temas y asignaturas de los currículos escolares.
Algunos de los temas que podemos encontrar, en éste y otros enlaces de Internet, son tareas como componer música, biología (estudio de los diferentes ecosistemas y de las consecuencias de la alteración climática de los mismos, reforestación de entornos, cambios en los hábitats animales, explorar el recorrido que la sangre hace a través del cuerpo), química (trabajo con los diferentes estados de la materia, elementos químicos, reacciones químicas), historia (aprendizaje y profundización de la vida cotidiana de civilizaciones), programación (circuitos y puertas lógicas) o literatura (relato de cuentos, fábulas).
En cuanto a las actividades matemáticas, las hay de todo tipo y condición, abarcando los más diversos temas: fracciones, números decimales, resolución de ecuaciones, rompecabezas en base diez (y otras bases), trabajo con patrones aritméticos para diseñar y crear estructuras arquitectónicas, factores y divisores, estadísticas, probabilidad.
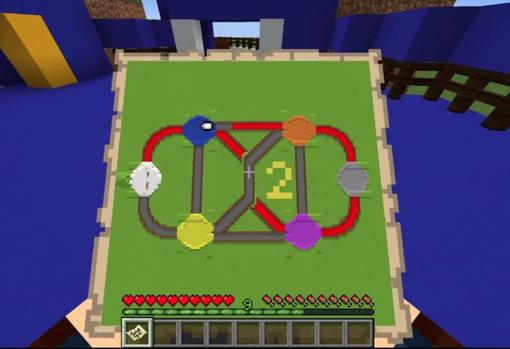
Pero se debe resaltar una utilidad de matemática no elemental, que ha sido diseñada por el matemático David Strütt. Se trata de Matheminecraft, con la que el jugador debe orientarse dentro de un laberinto tridimensional para encontrar un recorrido euleriano.
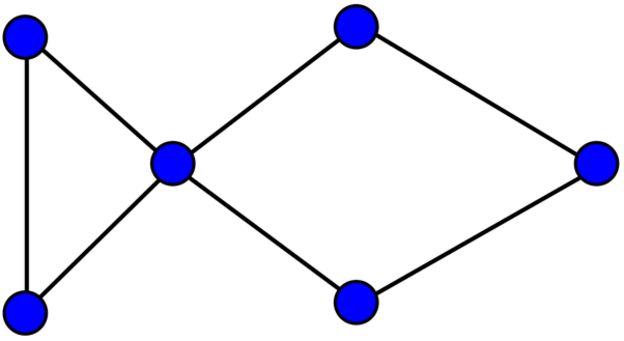
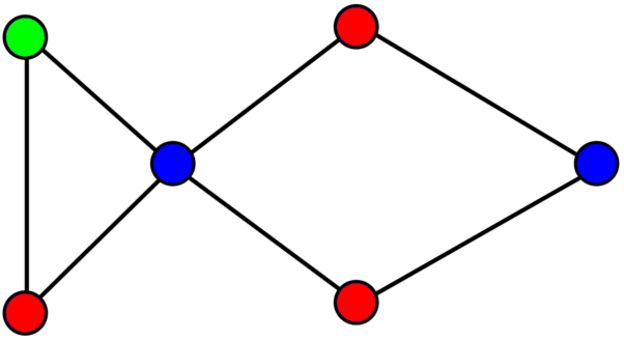
En la imagen superior se ve un grafo euleriano. La teoría de grafos es un tema muy frecuentado por los artículos de divulgación matemática. Tiene su origen en el siglo XVIII, en concreto cuando al matemático Leonhard Euler le plantearon en 1736 los habitantes de la ciudad de Königsberg (hoy Kaliningrado, en Rusia) si sería posible recorrer los siete puentes que la localidad tenía sobre el río Pregel una vez y sólo una, sin pasar dos veces por el mismo punto y acabar en el punto de partida.
Euler demostró que no era posible, que ese problema no tenía solución. Pero lo interesante no fue la resolución, sino que para probarlo utilizó un método novedoso, a base de puntos y segmentos, que resultó un procedimiento aplicable a otras muchas situaciones.
Minecraft, fue concebida con un tutorial y cuatro niveles. Pensada inicialmente como atracción en un evento llamado Open Days en 2009, sus responsables decidieron extender su propuesta a un ámbito mayor.
En Matheminecraft cada nivel consiste en un gráfico que admite un ciclo euleriano. El juego usa gráficos sencillos, de modo que los jugadores encontrarán prácticamente con seguridad el ciclo euleriano.
En la actualidad, se están preparando niveles adicionales y nuevas series de talleres que tendrán lugar a finales de 2020 y 2021. Y aparecerá un Matheminecraft 2.0 en el que el jugador tendrá que elegir el punto de partida de su ciclo.
Fuente y más información:
Filed under: Matemáticas y juego | Tagged: juego, matheminecraft, minecraft, Teoría de Grafos | Leave a comment »